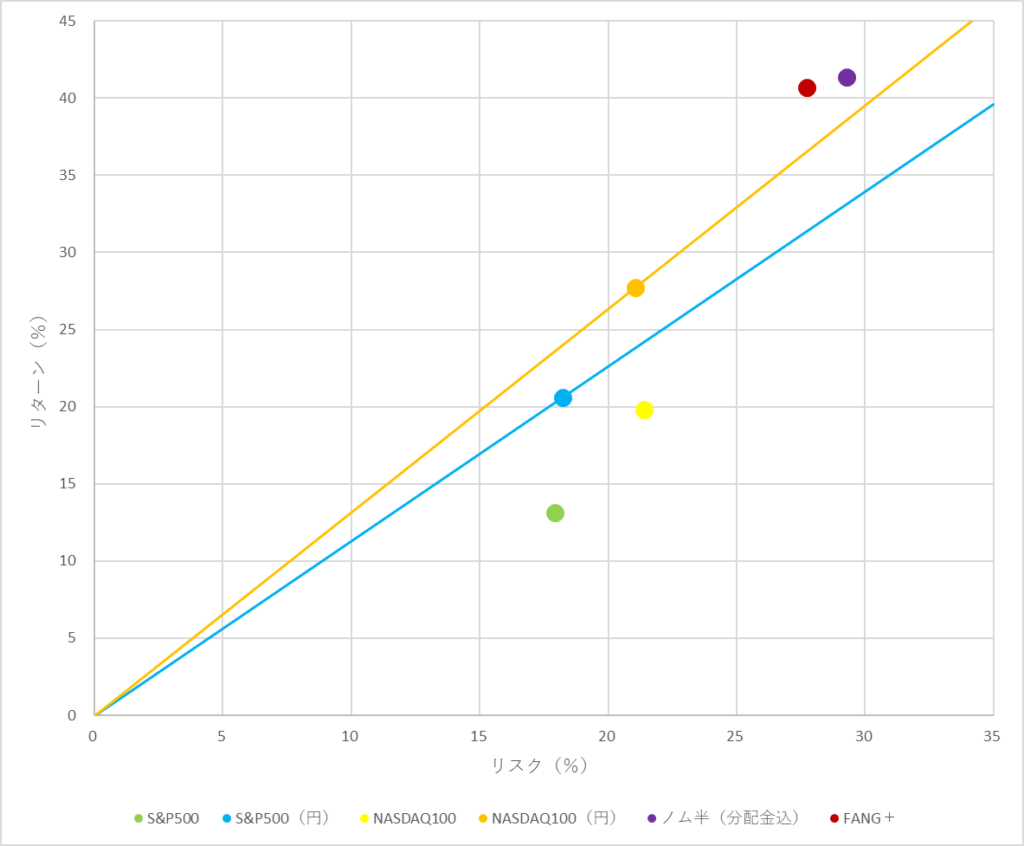
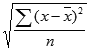こんにちは〜🌤️おりおりです🙋♀️
計算式とエクセル関数
投資について調べていると良く出てくるのが、リターンとリスクの数字です。
これがどうやって算出されているのか、結論から言うと以下の通りです。
厳密に言うと、年率換算(年間での変化率を計算)したものですが、(特に表記がなければ)これが一般的だと思います。
では、なぜこうなるのか、もう少し詳しく見てみましょう。
丸暗記しなくても経緯を知っていると覚えられるね

リターン(年率)の求め方
リターンとは、ある時期を基準として、何%上がったか(下がったか)を表す数字です。
ですので、+20%と言うと120%、つまり1.2倍になったという意味です。
では、ここからさらに+20%になったらどうなるかと言うと 20% + 20% = 40% ではなく、1.2倍の1.2倍ですから、1.44倍(+44%)です(これが複利というやつです)。
これが続くと、1.2 × 1.2 × 1.2 × ... と続き、掛けた回数に応じて、1.2 ^ 3(1.2 の 3乗)や 12 ^ 4(1.2 の 4乗)などと表現されます。
例えば、リターン(年率)が20%の状態が10年続いた場合はと言うと、元の値の 1.2 ^ 10 = 6.1917... 倍になります(Excelでは「=POWER(1.2,10)」)。
では逆に、10年で5倍(+400%)になった場合のリターン(年率)はいくらでしょうか。
A ^ 10 = 5 を解くと、A = 5 ^ (1 / 10) = 5 ^ 0.1(5 の 0.1乗)= 1.1746... となります。
(この数字を10乗すると5になることで検算ができます)
これをリターン(何%上がったか)にするには、1を引いた後に100を掛けて、(1.1746 - 1)× 100 = 17.46% になります 。
ですから、〇年前の基準価額からリターンを求めるには先ほどの式になるわけです。
ちなみに、〇には小数点以下を含めても(9年6ヶ月なら 9.5 としても)OKです。

複利の逆算っていうイメージね
リスクの求め方
これに対して、投資におけるリスクとは、収益率の振れの大きさを示す数値になります。
(必ずしもマイナスとは限らず、プラスに振れる方も含みます)
計算方法としては、一般的に下記のような標準偏差が使われます。
リスクの計算方法
資産運用の世界ではリスクを測る指標として、統計学の「標準偏差」(ひょうじゅんへんさ)を一般的に用いています。標準偏差と言うと難しく聞こえるかも知れませんが、要は「収益が上下にどれだけ変動するかを数値化したもの」です。標準偏差の計算方法は、下図で紹介しています。
でも、難しければ「こんなふうに計算するんだ」というぐらいの理解で十分です。具体的な計算方法よりも、標準偏差の見方を覚えて実際の資金運用において役立てることのほうが重要です。
投資リスクの計算方法 | auのiDeCo(イデコ)
こちらは、開始と終了(現在)だけではなく、一定期間(1日、1週間、1ヶ月など)ごとのリターンのデータが必要です。
そして、それぞれのデータから平均値を引いて2乗したものを足し合わせ、データ数で割った(平均を取った)後、平方根を求めます。
(手動だと面倒ですが、Excelだと STDEVP 関数 で一発です)
STDEVP 関数は次の数式を使って標準偏差を計算します。
STDEVP 関数 - Microsoft サポート
上記で一定期間におけるリスクの値が出ますので、これを下記のルールで年率換算します。
(ランダム・ウォーク理論とは、「株価を予測することはできない」とする理論のことです)
標準偏差は求めた値を年率換算(年間での変化率を計算)して使うのが一般的だ。具体的には、日次、週次、月次騰落率から計測した標準偏差について、1年=250(営業日)=52(週)=12(月)の各250、52、12の平方根を掛けた値が年率換算値になる。それぞれの平方根を掛け合わせるのは、標準偏差の2乗である分散が計測期間(時間)の長さに比例して大きくなるというランダム・ウォークの考え方に基づく。
標準偏差・分散|証券用語解説集|野村證券
Excelでは平方根は SQRT 関数 ですから、これをまとめると最初の式になります。
騰落率とは(【その時点の基準価額】-【前日 or 前週 or 前月の基準価額】- 1)× 100 です。
ランダムウォーク理論では、このリスクの数字が大きいほど、リターンの中央値が押し下げられるらしいよ

散布図で視覚的に
一般的に、リターンは高い方が、リスクは低い方が優秀な投資先とされています。
それを見やすくするために、散布図が良く使われます。
(リターンを縦軸、リスクを横軸に取り、 各々の銘柄を平面上にプロット)
こちらも、Excel(のグラフ機能)を使うと簡単です。
S&P500とNASDAQ100(ドル・円)の指数値、および高リスクファンドの中でも運用期間が長い「野村世界業種別投資シリーズ(世界半導体株投資)」(ノム半)と「iFreeNEXT FANG+インデックス」(FANG+)の基準価額の過去5年と10年のデータ(月単位)を使い、
上記の方法でリターンとリスクを求め、散布図を作成するとこうなります。
(FANG+は設定日が2018年1月のため、後者は6.5年で計算しています)
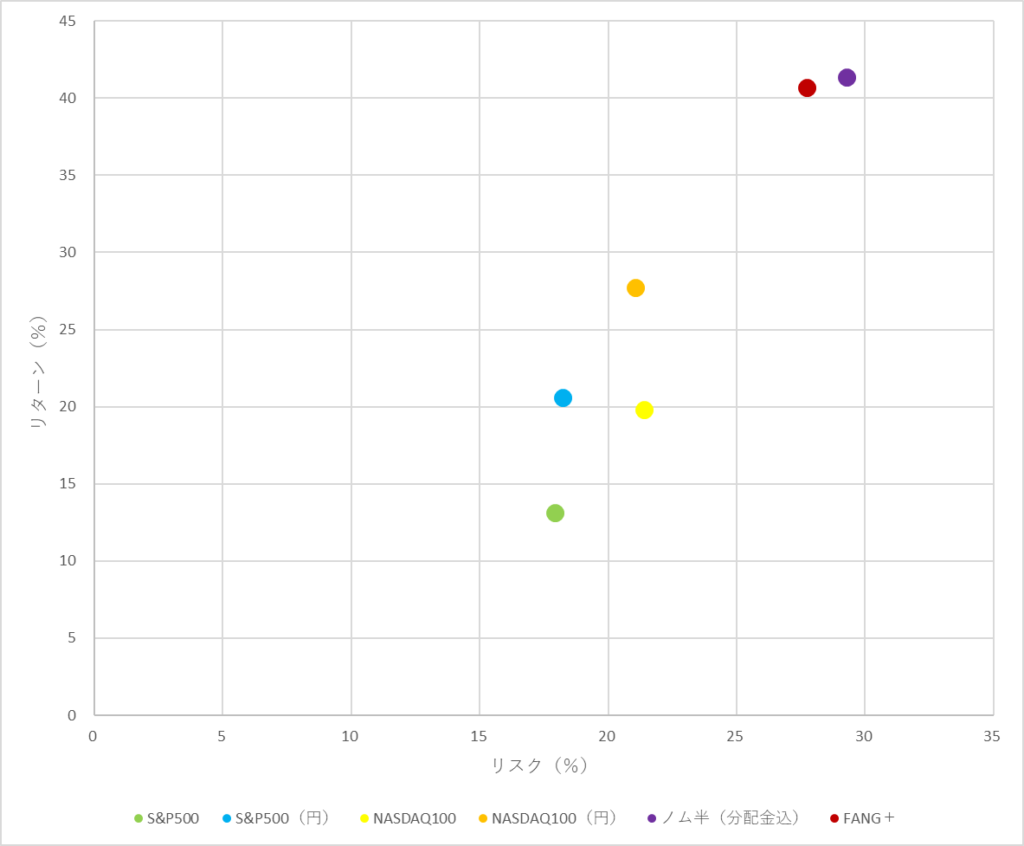
この図で、左上にあればあるほど優秀(低リスク・高リターン)で、右下にあればあるほどイマイチ(高リスク・低リターン)となります。
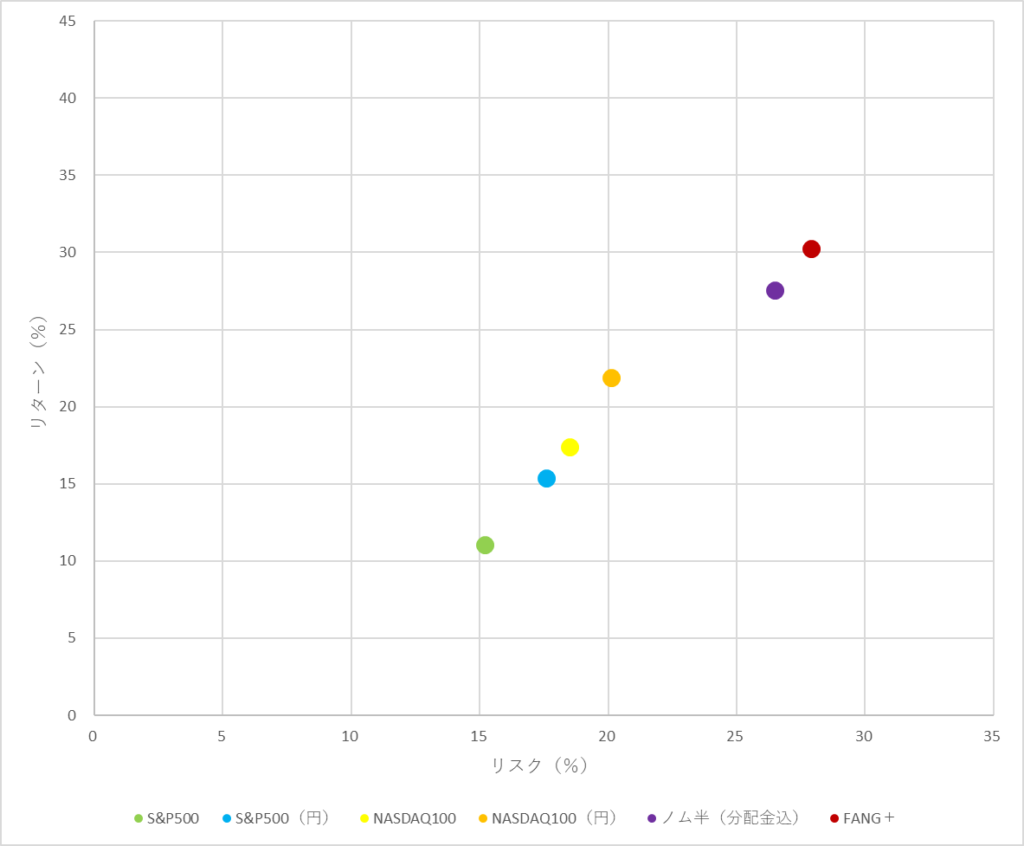
このように、基準にしたいものに原点(0, 0)から直線を引くとより分かりやすくなります。
(Excelでは、「0」「35」の列と「0」「35 × リターン / リスク」の列を追加し、グラフにもこれをデータソースとして「散布図 (直線)」を別途追加します)
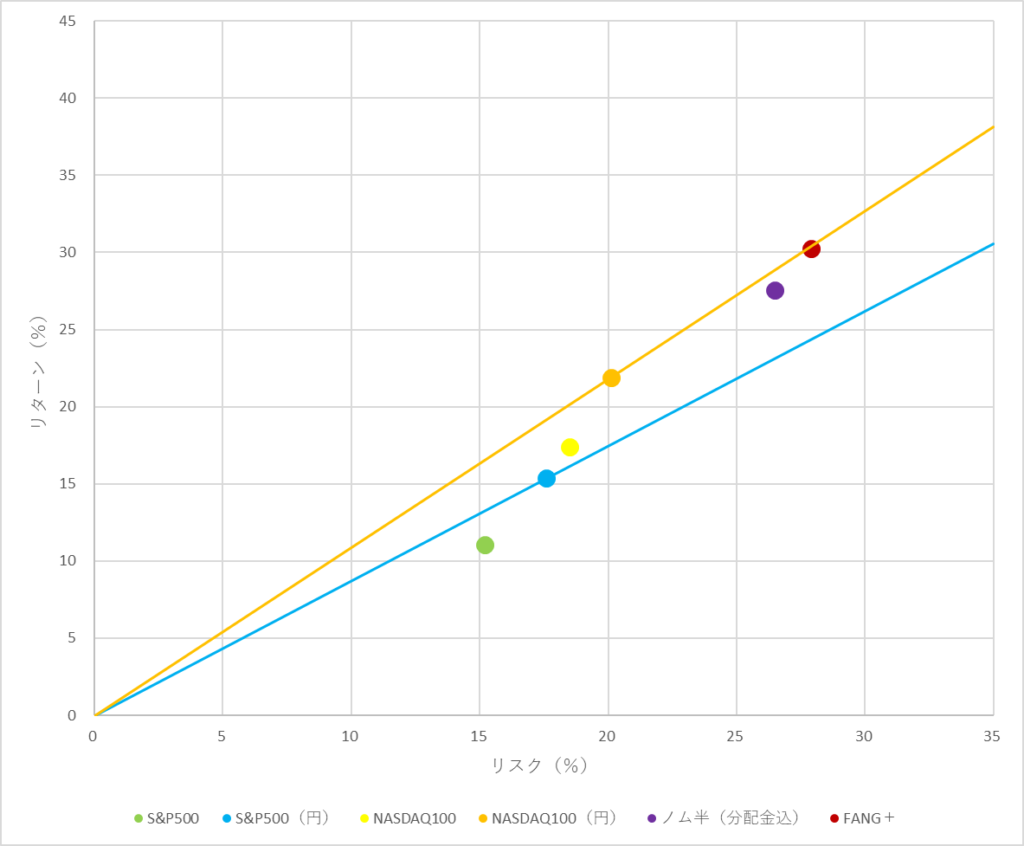
これを見ると、ノム半やFANG+は過去5年間ではS&P500やNASDAQ100より上ですが、10年間ではNASDAQ100に劣後することが分かります。
このように、データの期間によって結果が変わるのはチャートなどと同じですし、そもそも過去は未来を保障しないため鵜呑みは厳禁ですが、指数やファンドを評価するにあたって、ひとつの指標としては大いにアリかと思います。

原点から結んだ線より上にあれば優秀ってわけね
それでは皆様、よきフィットネスライフを〜🏃♀️